Radiocarbon dating (or simply carbon dating) is a radiometric dating technique that uses the decay of carbon-14 (14C) to estimate the age of organic materials, such as wood and leather, up to about 58,000 to 62,000 years Before Present (BP, present defined as CE 1950).[1] Carbon dating was presented to the world by Willard Libby in 1949, for which he was awarded the Nobel Prize in Chemistry.
Since the introduction of carbon dating, the method has been used to date many items, including samples of the Dead Sea Scrolls, the Shroud of Turin, enough Egyptian artefacts to supply a chronology of Dynastic Egypt,[2] and Ötzi the Iceman.[3]
The Earth's atmosphere contains various isotopes of carbon, roughly in constant proportions. These include the main stable isotope (12C) and an unstable isotope (14C). Through photosynthesis, plants absorb both forms from carbon dioxide in the atmosphere. When an organism dies, it contains the standard ratio of 14C to 12C, but as the 14C decays with no possibility of replenishment, the proportion of carbon 14 decreases at a known constant rate. The time taken for it to reduce by half is known as the half-life of 14C. The measurement of the remaining proportion of 14C in organic matter thus gives an estimate of its age (a raw radiocarbon age).[4] However, over time there are small fluctuations in the ratio of 14C to 12C in the atmosphere, fluctuations that have been noted in natural records of the past, such as sequences of tree rings and cave deposits. These records allow fine-tuning, or "calibration", of the raw radiocarbon age, to give a more accurate estimate of the calendar date of the material. One of the most frequent uses of radiocarbon dating is to estimate the age of organic remains from archaeological sites.
Physical and chemical background[edit]
Carbon has two stable, nonradioactive isotopes: carbon-12 (12C), and carbon-13 (13C), and a radioactive isotope, carbon-14 (14C), also known as radiocarbon. The half-life of 14C (the time it takes for half of a given amount of 14C to decay) is about 5,730 years, so its concentration in the atmosphere might be expected to reduce over thousands of years. However, 14C is constantly being produced in the lower stratosphere and upper troposphere by cosmic rays, which generate neutrons that in turn create 14C when they strike nitrogen-14 (14N) atoms.[5]
The carbon dating process is described by the following nuclear reaction, where n represents a neutron and p represents a proton:[6]
Once produced, the 14C quickly combines with the oxygen in the atmosphere to form carbon dioxide (CO
2). Carbon dioxide produced in this way diffuses in the atmosphere, is dissolved in the ocean, and is taken up by plants via photosynthesis. Animals eat the plants, and ultimately the radiocarbon is distributed throughout the biosphere. The combination of the ocean, the atmosphere and the biosphere is referred to as the carbon exchange reservoir.[7]
2). Carbon dioxide produced in this way diffuses in the atmosphere, is dissolved in the ocean, and is taken up by plants via photosynthesis. Animals eat the plants, and ultimately the radiocarbon is distributed throughout the biosphere. The combination of the ocean, the atmosphere and the biosphere is referred to as the carbon exchange reservoir.[7]
If it is assumed that the cosmic ray flux has been constant over the last ~100,000 years, then carbon-14 has been produced at a constant rate, and since it is also lost through radioactivity at a constant rate, the proportion of radioactive to non-radioactive carbon is constant. The ratio of 14C to 12C in the carbon exchange reservoir is 1.5 parts of 14C to 1012 parts of 12C.[7] In addition, about 1% of the reservoir is made up of the stable isotope13C.[5]
Invention of the methods[edit]
In the mid-1940s, Willard Libby, then at the University of Chicago, realized that the decay of carbon-14 might lead to a method of dating organic matter. Libby published a paper in 1946 in which he proposed that the carbon in living matter might include carbon-14 as well as non-radioactive carbon.[8][9] Libby and several collaborators proceeded to experiment with methane collected from sewage works in Baltimore, and after isotopically enriching their samples they were able to demonstrate that they contained radioactive carbon-14.
By contrast, methane created from petroleum had no radiocarbon activity. The results were summarized in a paper in Science in 1947, and the authors commented that their results implied it would be possible to date materials containing carbon of organic origin.[8][10] Libby and James Arnold proceeded to experiment with samples of wood of known age.
For example, two wood samples taken from the tombs of two Egyptian kings, Zoser and Sneferu, independently dated to 2625 BC plus or minus 75 years, were dated by radiocarbon measurement to an average of 2800 BC plus or minus 250 years.[11][12] These measurements, published in Science in 1949, launched the "radiocarbon revolution" in archaeology, and soon led to dramatic changes in scholarly chronologies.[12] In 1960, Libby was awarded the Nobel Prize in chemistry for this work.[13]
Calculating ages[edit]
While a plant or animal is alive, it is exchanging carbon with its surroundings, so that the carbon it contains will have the same proportion of 14C as the biosphere. Once it dies, it ceases to acquire 14C, but the 14C that it contains will continue to decay, and so the proportion of radiocarbon in its remains will gradually reduce. Because 14C decays at a known rate, the proportion of radiocarbon can be used to determine how long it has been since a given sample stopped exchanging carbon—the older the sample, the less 14C will be left.[7]
The equation governing the decay of a radioactive isotope is[5]
where N0 is the number of atoms of the isotope in the original sample (at time t = 0), and N is the number of atoms left after time t.[5] λ is a constant that depends on the particular isotope; for a given isotope it is equal to the reciprocal of the mean-life—i.e. the average or expected time a given atom will survive before undergoing radioactive decay.[5] The mean-life, denoted by τ, of 14C is 8,267 years, so the equation above can be rewritten as:[14]
The ratio of 14C atoms in the original sample, N0, is taken to be the same as the ratio in the biosphere, so measuring N, the number of 14C atoms currently in the sample, allows the calculation of t, the age of the sample.[7]
The half-life of a radioactive isotope (the time it takes for half of the sample to decay, usually denoted by T1/2) is a more familiar concept than the mean-life, so although the equations above are expressed in terms of the mean-life, it is more usual to quote the value of 14C's half-life than its mean-life. The currently accepted value for the half-life of radiocarbon is 5,730 years.[5] The mean-life and half-life are related by the following equation:[5]
The above calculations make several assumptions: for example, that the level of 14C in the biosphere has remained constant over time.[15] In fact, the level of 14C in the biosphere has varied significantly and, as a result the values provided by the equation above, have to be corrected by using data from other sources, using a calibration curve, which is described in more detail below.[16] For over a decade after Libby's initial work, the accepted value of the half-life for 14C was 5,568 years; this was improved in the early 1960s to 5,730 years, which meant that many calculated dates in published papers were now incorrect (the error is about 3%). However, it is possible to incorporate a correction for the half-life value into the calibration curve, and so it has become standard practice to quote measured radiocarbon dates in "radiocarbon years", meaning that the dates are calculated using Libby's half-life value and have not been calibrated.[17] This approach has the advantage of maintaining consistency with the early papers, and also avoids the risk of a double correction for the Libby half-life value.[18]


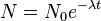


No comments:
Post a Comment